
Cuaderno Familia de NÚMEROS

En el transcurso de la historia, familia de números surgieron naturalmente para contar (números cardinales: uno, dos, tres, etcétera) y, a la vez, para ordenar (números ordinales: primero, segundo, tercero, etcétera). Por este motivo, el primer conjunto de números que aparece es el de los números naturales.
Materiales ACTIVIDADES DE LOS NÚMEROS
Es razonable comenzar cualquier estudio de los números con ellos, porque los números naturales están en la base de todos los otros conjuntos. Sin embargo, con el tiempo aparecieron nuevos usos para los números y, con los usos, nuevos números.
Familia de números naturales se pueden sumar y multiplicar. Y, a veces, se pueden restar. Sin embargo, no se puede restar a un número natural otro mayor, porque el resultado ya no es un número natural. Es así como, para poder restar, se necesitan el cero y los números negativos.
A la humanidad le tomó siglos aceptar estos nuevos números, pese a que pasan a tener un sentido muy concreto cuando se los usa, por ejemplo, para expresar deudas. Hoy en día, los números negativos son de uso cotidiano. Los naturales dan lugar así a los enteros. Con los enteros se puede multiplicar, sumar y restar.
👇Material disponible en PDF 👉 Familia de Números

Hoy en día, muchas de las propiedades de los números enteros se expresan, de manera muy satisfactoria, usando enteros modulares. Si bien estos conjuntos aparecieron definidos de manera clara hace poco tiempo (desde una perspectiva histórica), su uso permite entender más cabalmente a los números enteros, y por ello les dedicamos un capítulo. Sin embargo, los números enteros no permiten divisiones si no se está dispuesto a tener resto.
Si trabajamos en geometría, incluso si se adoptan unidades de medida tales que las cantidades a medir sean enteras, poco se podrá hacer si no se utilizan fracciones, es decir sin introducir los números racionales. Por ejemplo, el Teorema de Tales habla de longitudes proporcionales, que inmediatamente dan lugar a las fracciones.
Imagen referencial del material👇 Familia de Números
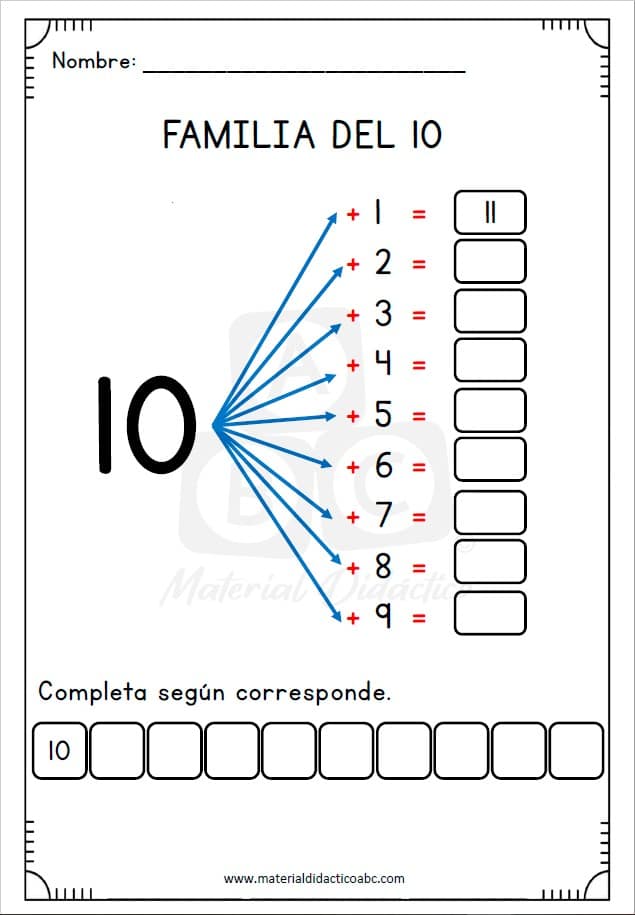
Link Material: Cuaderno Familia de NÚMEROS
La suma y el producto de números naturales son operaciones conmutativas y asociativas. El producto tiene un elemento neutro, que es el número uno. La suma, en cambio, no lo tiene, si se considera que el cero no pertenece al conjunto de los naturales. En cambio, si agregamos el cero a los números naturales, éste resulta ser el elemento neutro de la suma.
Imagen referencial del material👇 Familia de Números
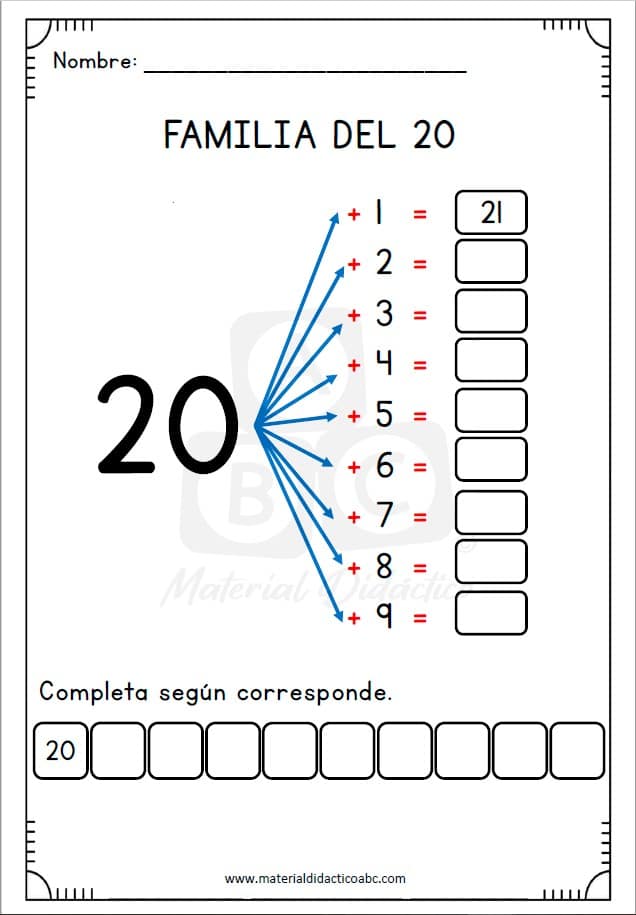
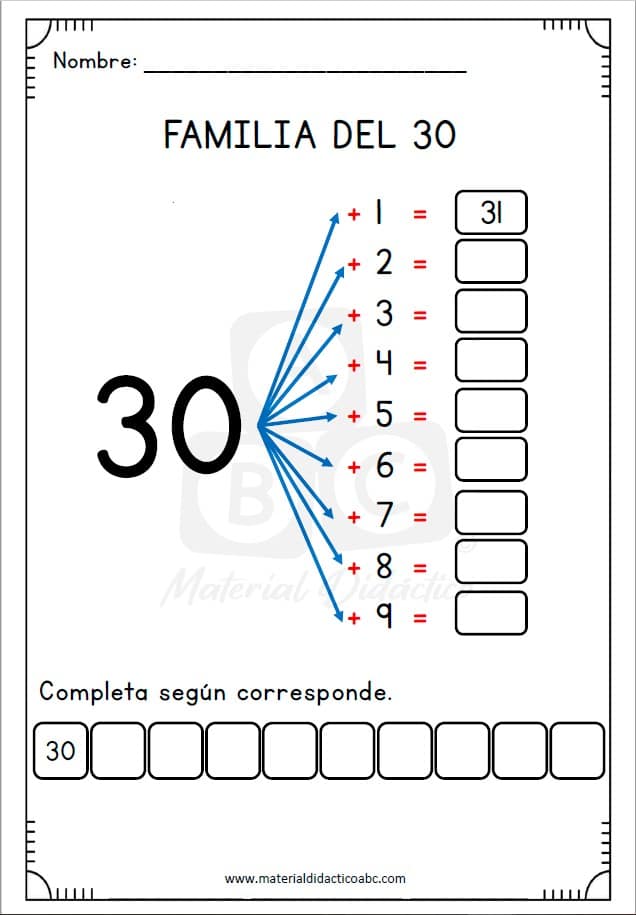
Por lo que respecta a los números y las operaciones, aprenden a contar, recitar la secuencia numérica; a reconocer las cifras y escribirlas; a coordinar y comparar conjuntos de objetos, a decir cuántos objetos hay, dónde hay más o menos; a expresar simbólicamente estas relaciones; a sumar con los dedos, o mediante la recta numérica, o con regletas de colores; a distinguir entre valor absoluto y relativo de las cifras, asociando la posición con el orden de la unidad y adentrándose con ello, por tanto, en la comprensión del sistema de numeración.
También dedican su tiempo a escribir sumas de forma standard y realizarlas en el papel; a memorizar las tablas de sumar –o, más adelante, multiplicar–; y aprenden un conjunto de hechos numéricos producto de estas y otras tareas como contar a saltos, componer y descomponer números, etc.
Familia de Números de contar. Para empezar, es el desenvolvimiento en el tiempo de la sucesión de los números naturales, cuyos primeros pasos son tan arduos para los niños como aprender los nombres de los colores y de las letras, hasta que aprehenden de repente la secuencia como totalidad que continúa ilimitadamente una aprehensión conceptual que no tiene su análogo en el aprendizaje de los nombres de los colores y las letras.
Familia de números de contar se convierte en el objeto irreemplazable de la actividad de calcular. Pronto se siente la necesidad de contar hacia atrás, hacia el pasado, esto es, mediante números negativos. El número de contar, llamado matemáticamente el número ordinal, se formaliza en la inducción completa, y ulteriormente en los axiomas de Peano; su apoteosis son los ordinales transititos.












